Simulating Data

Random Numbers, Distributions, and Patterns

Author

Raju Rimal

Published

November 30, 2024

Modified

March 19, 2025

Simulation is a powerful tool in R that allows users to generate synthetic data for various purposes, such as testing algorithms, validating statistical methods, or modeling hypothetical scenarios. This blog explores how to simulate different types of data in R, ranging from basic numeric data to complex datasets mimicking real-world scenarios.

1. Why Simulate Data?

Simulating data can be useful for:

  • Testing and Debugging: Quickly test hypotheses, methods, or functions.
  • Comparing Methods: Evaluate the performance of statistical or machine learning models.
  • Educational Purposes: Illustrate theoretical concepts or principles.
  • Model Validation: Simulate edge cases or scenarios that might be rare in real-world data.

2. Simulating Basic Numeric Data

A. Random Numbers

R provides a suite of functions for generating random numbers from various distributions.

Distributions

# Generate 10 random numbers between 0 and 1
runif(10, min = 0, max = 1)
 [1] 0.5381849 0.1762189 0.8714240 0.8766567 0.7341599 0.6023519 0.1306099
 [8] 0.1659936 0.9104378 0.7376089
# Generate 10 random numbers with mean = 0, sd = 1
rnorm(10, mean = 0, sd = 1)
 [1]  0.86461297  0.27353752 -0.47053425 -0.19664722 -0.45950327 -0.23119203
 [7]  1.03159373 -0.03357540 -1.26013695  0.04818279
# Generate 10 random numbers with lambda = 5
rpois(10, lambda = 5)
 [1] 2 5 4 2 0 6 2 5 3 3

B. Sequences and Patterns

# Sequence from 1 to 10
seq(1, 10, by = 1)
 [1]  1  2  3  4  5  6  7  8  9 10
# Repeating numbers
rep(1:3, times = 3)    # Repeats the sequence 1, 2, 3 three times
[1] 1 2 3 1 2 3 1 2 3
rep(1:3, each = 2)     # Repeats each number twice
[1] 1 1 2 2 3 3

3. Simulating Categorical Data

A. Using Factors

# Simulate a categorical variable with 3 levels
categories <- sample(c("A", "B", "C"), size = 10, replace = TRUE)
categories <- factor(categories)
print(categories)
 [1] C C A B B A C A C A
Levels: A B C

B. Weighted Categories

# Simulate with unequal probabilities
weighted_categories <- sample(c("A", "B", "C"), size = 10, replace = TRUE, prob = c(0.5, 0.3, 0.2))
print(weighted_categories)
 [1] "A" "B" "A" "B" "C" "A" "A" "A" "B" "C"

4. Simulating Time-Series Data

A. Random Walk

# Simulate a random walk
set.seed(123)
n <- 100
random_walk <- cumsum(rnorm(n))
plot(random_walk, type = "l", main = "Random Walk")

B. Seasonal Data

# Simulate seasonal data with noise
time <- 1:100
seasonal_data <- 10 * sin(2 * pi * time / 12) + rnorm(100, sd = 2)
plot(time, seasonal_data, type = "l", main = "Seasonal Data")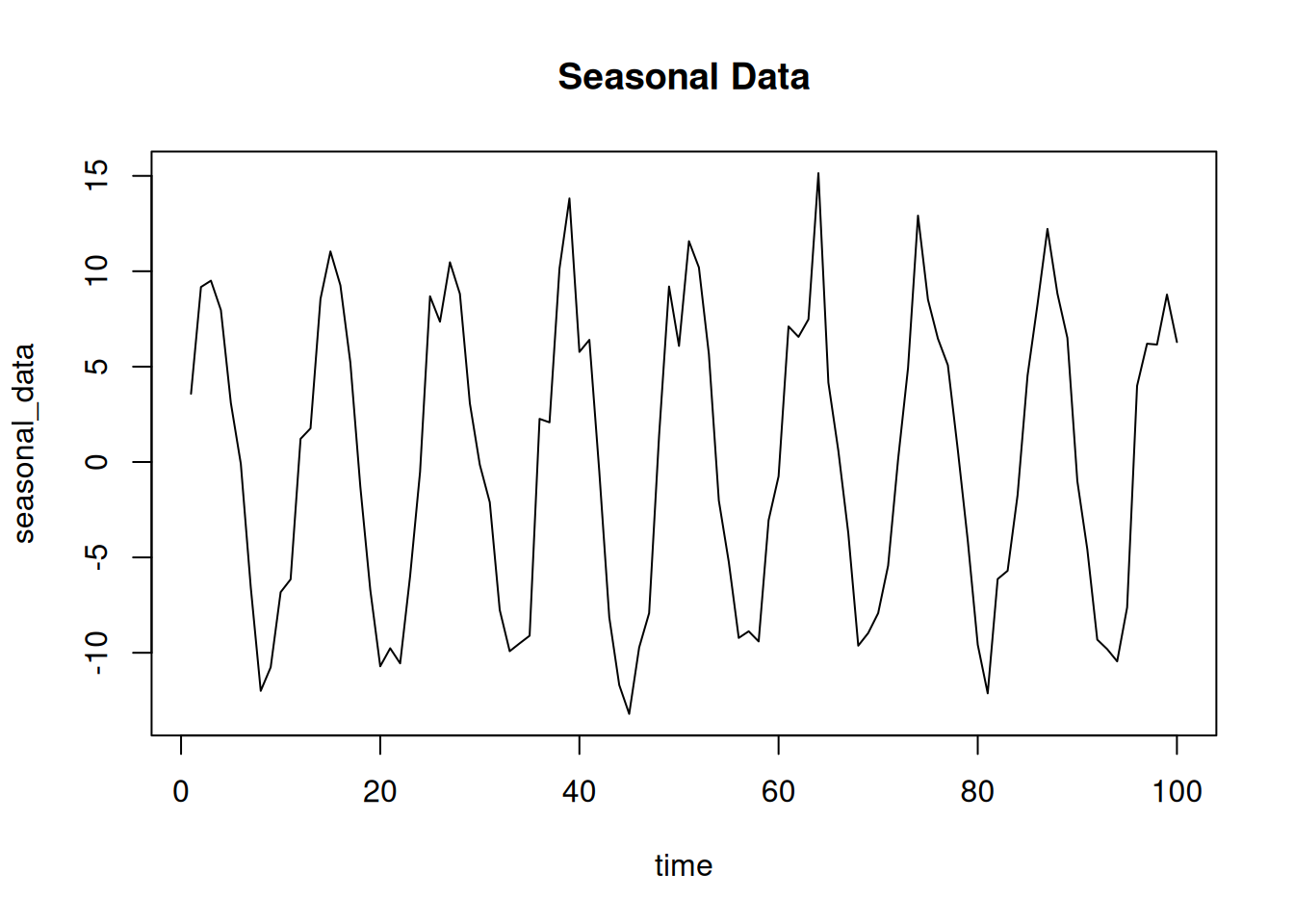

5. Simulating Multivariate Data

A. Multivariate Normal Distribution

library(MASS)

# Define mean vector and covariance matrix
mu <- c(0, 0)
sigma <- matrix(c(1, 0.5, 0.5, 1), nrow = 2)

# Generate 100 samples
multivariate_data <- mvrnorm(n = 100, mu = mu, Sigma = sigma)
print(head(multivariate_data))
           [,1]        [,2]
[1,]  2.2618467  1.54660453
[2,]  1.5129275  0.76023849
[3,]  0.2396470 -0.69889171
[4,]  0.9966765 -0.05583679
[5,] -0.1402492 -0.57740869
[6,] -0.5780315 -0.24685232

B. Correlated Data

# Generate correlated data
set.seed(123)
x <- rnorm(100)
y <- 0.8 * x + rnorm(100, sd = 0.5)

plot(x, y, main = "Correlated Data")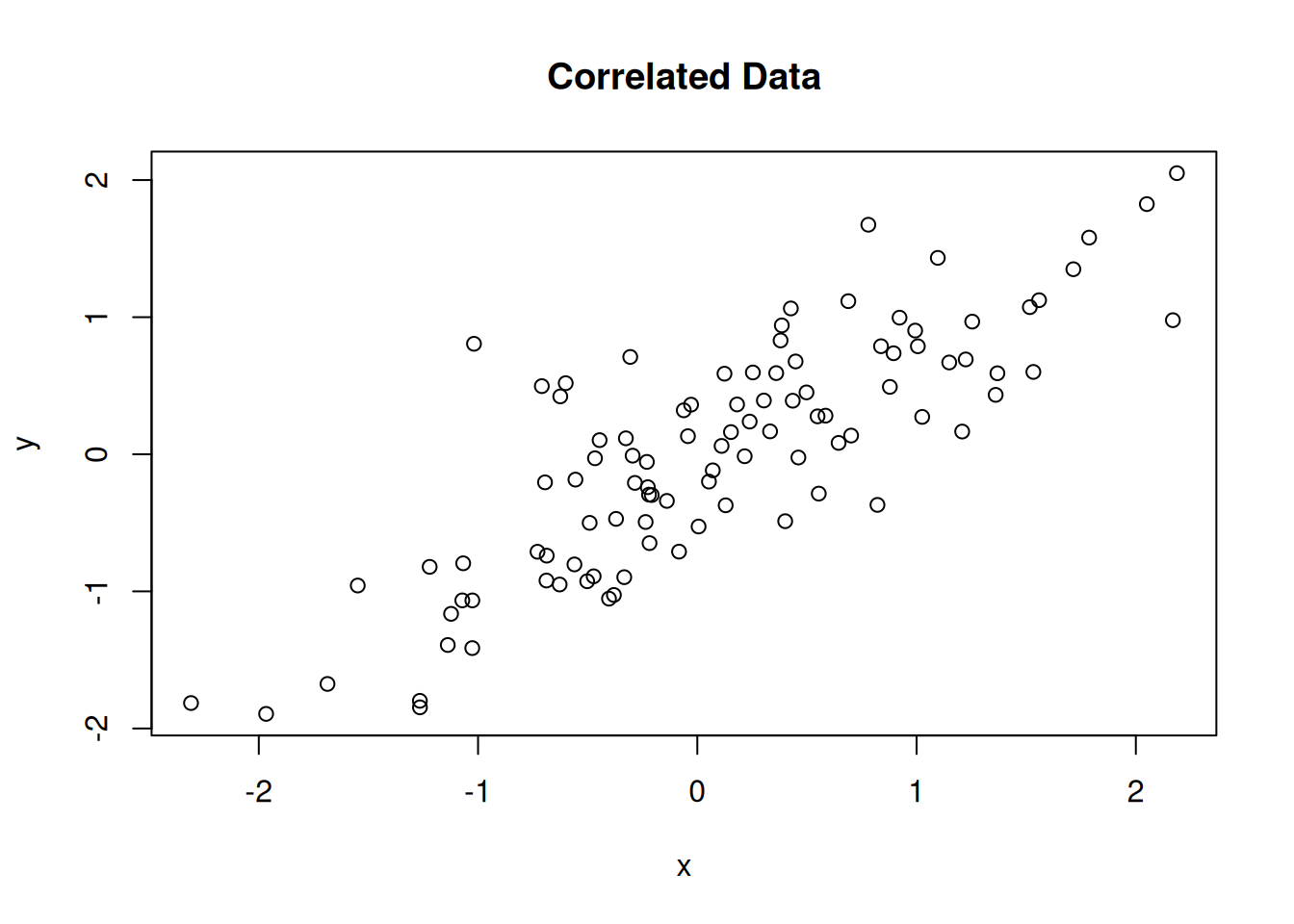

6. Simulating Complex Datasets

A. Simulating a Data Frame

set.seed(123)

# Simulate a dataset with multiple types of variables
data <- data.frame(
  ID = 1:100,
  Age = sample(20:60, 100, replace = TRUE),
  Gender = sample(c("Male", "Female"), 100, replace = TRUE),
  Income = rnorm(100, mean = 50000, sd = 10000),
  Passed = sample(c(TRUE, FALSE), 100, replace = TRUE)
)
print(head(data))
  ID Age Gender   Income Passed
1  1  50   Male 52353.87  FALSE
2  2  34 Female 50779.61  FALSE
3  3  33   Male 40381.43  FALSE
4  4  22   Male 49286.92   TRUE
5  5  56   Male 64445.51  FALSE
6  6  33   Male 54515.04  FALSE

B. Simulating Missing Data

# Add missing values to the Income column
data$Income[sample(1:100, 10)] <- NA
print(head(data))
  ID Age Gender   Income Passed
1  1  50   Male 52353.87  FALSE
2  2  34 Female 50779.61  FALSE
3  3  33   Male 40381.43  FALSE
4  4  22   Male 49286.92   TRUE
5  5  56   Male 64445.51  FALSE
6  6  33   Male       NA  FALSE

7. Practical Examples

A. Monte Carlo Simulation

Monte Carlo simulations involve repeated random sampling to compute a result.

Example: Estimating π

set.seed(123)

# Simulate random points
n <- 10000
x <- runif(n, -1, 1)
y <- runif(n, -1, 1)

# Points inside the unit circle
inside_circle <- x^2 + y^2 <= 1
pi_estimate <- 4 * sum(inside_circle) / n
print(pi_estimate)
[1] 3.1576

B. Bootstrapping

Bootstrapping involves resampling a dataset to estimate statistics.

set.seed(123)

# Original data
original_data <- rnorm(100, mean = 50, sd = 10)

# Bootstrap resamples
resamples <- replicate(1000, mean(sample(original_data, replace = TRUE)))
hist(resamples, main = "Bootstrap Means")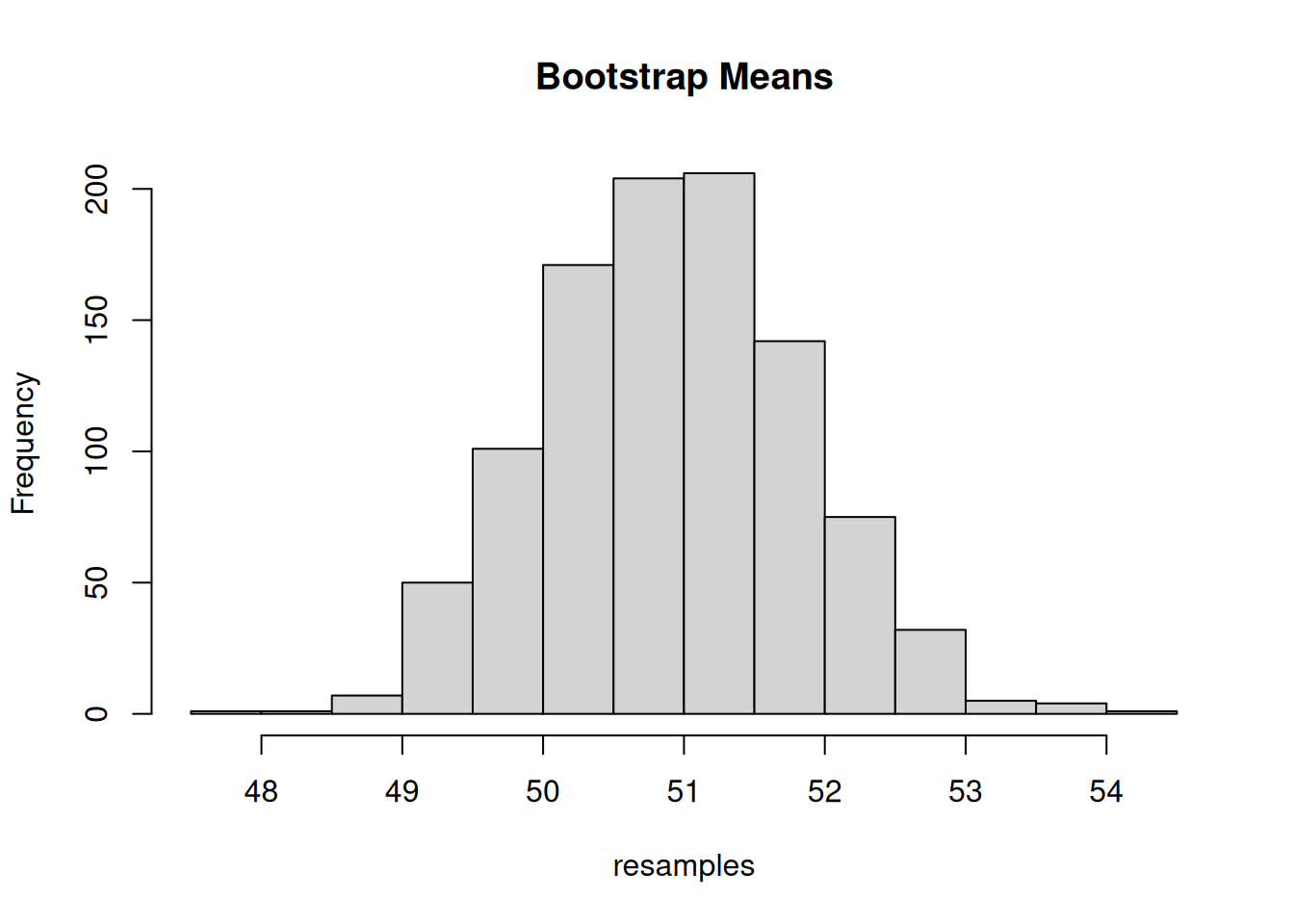

8. Tips for Simulating Data

  1. Set a Seed: Use set.seed() to ensure reproducibility of random data.
  2. Validate Simulated Data: Check the structure and properties of simulated data to ensure they meet your requirements (e.g., mean, variance).
  3. Start Simple: Build simple simulations before incorporating complex dependencies.
  4. Automate with Functions: Create reusable functions for frequently used simulation tasks.

9. Practice Exercise

  1. Simulate a dataset with the following structure:
    • 100 observations.
    • A numeric variable following a normal distribution.
    • A categorical variable with 3 levels and unequal probabilities.
    • A binary variable (TRUE/FALSE).
  2. Introduce 10% missing data into one of the columns.
  3. Plot a histogram for the numeric variable and a bar plot for the categorical variable.

Conclusion

Simulating data in R is an essential skill that allows you to test ideas, compare methods, and better understand statistical principles. By mastering these techniques, you can create synthetic datasets tailored to your needs, whether for research, teaching, or debugging.